第0章 课程导学
一、什么是嵌入式
以引用为中心、计算机基础为基础、==软硬件可裁剪==、==低功耗==、低体积、低成本、稳定性有严格要求的专用计算机系统
软硬件可裁剪:
软件方面 : 根据不同的硬件、产品、需求,去增加或删除设备
修改驱动 根据硬件工程师的电路和芯片的选型,怎么去做软件的适配
硬件方面: 根据不同的、产品、需求,去增加或删除设备
修改硬件外设 根据不同的工况选择不同的芯片
低功耗:
例如ARM系列芯片 可以根据不同的应用场景去改变芯片的主频
ARM 是一家公司 做方案的
架构熟悉之后 -> 软件方面 驱动适配
因特尔 AMD - > x86 x64 优点 性能高 缺点 贵 能耗高
ARM -> A R M 32 64
STM32
A系列 - > 高性能 MPU STM32MP157
R系列 - > 高稳定性 高实时性
M系列 -> 单片机 MCU
MAC M1
例如:在开发STM32的时候,配置某一模块,我都需要开启这个模块的时钟
硬件系统:运算器、控制器、存储器、输入设备、输出设备
地址总线、控制总线、数据总线
MCU CPU GPU MPU
MCU 单片机 --> CPU + 存储设备 + 输入输出设备
CPU 中央处理器 --> 控制 计算 少量 复杂
GPU 图形处理器 --> 控制 计算 大量 简单
MPU 能搭载系统的ARM架构芯片

软件系统:操作系统、应用程序
操作系统的各种功能:1、文件管理 2、进程管理 3、网络管理 4、内存管理 5、设备管理
文件管理 对于文件的管理 文本文件 、 套接字 、管道文件 、 设备文件
进程管理 多任务管理
网络管理 TCP/IP 、UDP 、 MQTT 、 http 网络编程 + C++
设备管理 字符设备管 块设备管理 驱动开发课程
二、数据结构都学什么
1、线性表
==顺序表(数组)、链表(指针)==
2、栈和队列
==栈和队列==
4、树
二叉树(创建、遍历(深度优先、广度优先)、释放
5、排序
三、为什么要学数据结构
1、 夯实C基础 3-400
2、 合理利用内存 提高程序效率
3、 构建工程思维
4、 你将超越同等语言基础 99% 的人·
四、如何学习数据结构
1、不怕难、不犯懒 敲代码 ==多写代码==
2、不急于敲代码,先画图 –> 伪代码 –> 写代码 –> 调试(70%)
3、 熟练掌握C开发、理解结构熟悉掌握 C 开发
五、知识点回顾
数组: 相同数据类型的封装,相同数据类型的有序集合
指针:指针就是地址数据 一级指针变量是存储普通变量空间地址的变量
函数:对代码封装,实现特定功能的一段代码
功能:函数的核心,可以实现什么功能
参数:需要参与功能运算的数据
返回值:返回运行结果
结构体:
不同数据类型的封装,是用户自定义数据类型,C语言为用户提供了一种程序员可以根据自己项目需要的数据类型,这种数据类型就是结构体
第一章 绪论
- 如何用程序代码把现实的问题信息化
- 如何用计算机高效的处理这些信息从而创造价值
二、基本概念和术语
2.1 基本概念和术语
2.1.1 数据
专家的理解:数据就是信息的载体,是描述客观事物属性的数、字符及所有能输入到计算机中并被计算机程序识别和处理的符号集合。
==所有可以输入到计算机中的信息集合==
2.1.2 数据元素
==数据元素==是数据的基本单位,通常位置一个整体进行考虑和处理,一个数据元素可以由若干个==数据项==所组成,数据项是构成数据元素的不可分割的最小单位。
2.1.3 数据对象
数据对象是具有相同性质的数据元素集合,是数据的一个子集。
是由==数据元素==和==数据项==所组成。
数据项 是不可拆分的最小单位
数据元素 由数据项所组成
typedef struct ElementData
{
char name[128]
int age;
int id;
}ElementData;
ElementData Data; // 数据元素 数据对象
Data.age; // 数据项
ElementData Data_arr[128]; // 数据对象
Data_arr[0] // 数据元素
Data_arr[0].age // 数据项
2.1.4 数据类型 ADT
数据类型是一个值的集合和定义在此集合上的一组操作的总称。
原子类型:不可再进行分割的的类型 int
结构类型:还可以再进行分割的数据类型 struct
抽象数据类型(ADT):抽象的数据组织及与之相关的操作 类 面向对象编程
抽象数据类型所描述的 是==数据对象==、==数据关系==、==基本操作==
数据对象:学生信息表
数据关系:逻辑关系:线性 存储关系: 顺序存储和非顺序存储
数据关系
小明 小红 小美 小张 小帅
第一种关系 去食堂打饭 一对一 线
小明 小红 小美 小张 小帅
第二种关系 班干部 一对多 树
小明 班长
小红 副班长 小美 副班长
小张 卫生委员 小帅 学习委员
第三种关系 关于班级的绯闻 多对多 图
小明 -> 小红
小红 -> 小明
小明 -> 小美
小美 -> 小帅
小张 -> 小美
小张 -> 小帅
基本操作:
增
删
改
查
判空
判满
排序
2.1.5 数据结构
数据结构是相互之间存在一种或者多种特定关系的数据元素集合。

2.2 数据结构的三要素
数据结构课程就是研究数据的==逻辑结构== 和 ==存储结构== 和 ==操作==

2.2.1 数据的逻辑结构

逻辑结构是指数据元素之间的逻辑关系, 即从逻辑关系上描述的数据,与数据的存储无关。
逻辑结构分为==线性==和==非线性结构==
==没关系==:集合
一对一:线性结构
有一个特点 :
除了最前面一个 和最后面一个 之外 每个元素都有唯一的一个直接前驱 和 一个后继

一对多:树形结构

多对多:图形结构、网状结构
多对多


2.2.2 数据的存储结构
存储结构是指数据结构在计算机中的表示,也叫==物理结构==。
顺序存储:要求逻辑上相邻的元素在物理位置上也相邻
举例子:数组
优点:便于查找 改
缺点: 对于 增 删 不方便

链式存储:要求逻辑上相邻的元素在物理位置上不一定相邻
优点:节省空间,防止内存碎片 便于增加 和 删除
缺点:不便于 查找 和 改
索引存储:在存储元素信息的同时,还建立附加索引表
优点:检索速度快
缺点:需要增加额外的空间来存放索引表,增加和删除也需要修改索引表

散列存储:根据元素的关键词直接计算出该元素的存储地址,又称为哈希存储
使用关键字 计算 存储的地址 key
优点:检索、增加、删除很快
缺点:如果==散列函数==不好,则可能出现元素单位的冲突
$F(x) = Y$
2.2.3 数据的操作
针对于数据对象所设计的操作
增、删、改、查、判空、判满….
结合逻辑结构、实际需求来定义基本运算
数据的增、删、改、查
运算的定义是针对逻辑结构的,指出运算的功能,
运算的实现是针对存储结构的,指出运算的具体操作步骤,
三、抽象数据类型的表示
用于描述 数据对象的 数据关系 和 这个关系之间的基本操作
ADT
数据对象
数据关系
基本操作
// 数据对象
typedef struct ElementData
{
char name[128]
int age;
int id;
}ElementData;
// 数据关系
typedef struct sql_list
{
ElementData data[128]; // 数据对象
int len;
}Sql_list;
线性表
顺序表 链表 栈 队列
// 基本操作
void Initlist(ElementData * L); // 创建
void MAX(int num1 , int num2); // 找最大值

四、算法的基本概念

4.1 什么是算法
算法是解决特定问题的一系列步骤和规则的有序集合,其目的是能够解决实际问题并得到期望的结果。在计算机科学中,算法是程序的核心,负责处理数据以达到所需的目标。
算法由两个重要组成部分组成:
- 数据结构(Data Structure):描述了数据的组织方式,以及如何在计算机内存中存储和访问数据。
- 算法(Algorithm):描述了解决问题的步骤和规则,以及如何使用数据结构进行高效地操作和处理数据。
举例来说,排序算法就是一种算法,它能够将一组数据按照一定的顺序进行排列,而数据结构则是存储这些数据的方式,如数组、链表等。
程序 = 数据结构 + 算法
数据结构 如何用数据正确的描述存在的问题并存入计算机
算法 如何高效的处理数据 以解决实际问题
算法是对特定问题求解的一种描述,他是指令的有限序列,其中每条指令表示一个或多个操作
如何将大象塞进冰箱里
- 1、打开冰箱
- 2、塞入大象
- 3、关闭冰箱
4.2 算法的特性
- 有穷性(Finiteness):算法必须在有限的步骤之后结束,每一步都可以在有限时间内完成。
- 确定性(Determinism):算法中每条指令必须有确切的含义,对于相同的输入,只能产生相同的输出。
- 可行性(Feasibility):算法必须能够正确实施,即能够解决实际问题。
- 输入/输出:算法可以有零个或多个输入,并产生一个或多个输出。
4.3 好算法的特征
正确性:算法能够正确的解决问题
可读性:算法应具有良好的可读性 加注释
健壮性:输入非法数据时,算法能够适当的做出反应或进行处理,而不会莫名其妙的输出结果
鲁棒性:在粗鲁的环境下还能由帮帮的特性 ==方式客户乱输入,防呆系统==
高效率和低存储需求
高效率 运算速度快 在同等的机器、语言、编译器 上 速度越快 越好
时间复杂度
低存储 省空间 占用内存空间少
空间复杂度
五、复杂度的计算
4.1 时间复杂度
时间复杂度:时间复杂度就是算法时间开销计算
思考:如何评估算法时间开销 -> 事后统计法
存在问题
1、和机器新能有关,如 : 超级计算机 Vs 单片机
2、和编程语言有关,越高级的语言执行效率就越低
3、和编译程序产生产生的机器码(可执行文件 二进制文件)质量有关
4、有些的算法是不能进行事后统计的 如 导弹控制算法
成本问题
算法时间复杂度 $T = T(n)$
事情发生前预估算法时间开销 $T(n)$ 与问题规模 $n$ 的关系(T 代表时间)
我们看一下下面这个程序
void loveYou(int n)
{
int i = 1;
while(i<=n)
{
i++;
printf("I Love You %d /n" , i);
}
printf("I Love You More Than %d\n" , n);
}
n = 9999
T(n) = 1 + 10000 + 10000 + 10000 + 1
T(n) = 3n + 3
T(n) = n
int main()
{
loveYou(9999);
}
从上面的代码我们不难看出,每行代码所执行的数量为
int i = 1; // 执行 1 次
while(i<=n) // 执行 3001 次
{
i++; // 执行 3000 次
printf("I Love You %d /n" , i); // 执行 3000 次
}
printf("I Love You More Than %d\n" , n); // 执行 1 次
上面代码所执行的效率 $T(n) = 3n + 3$
思考: 是否可以忽略表达式中某些部分?
$T (n) = 3n + 3$ — $n$ $O(n)$
$T(n) = n2 + 3n + 1000$ $n2$ $O(n^2)$ 高阶的项目数
$T(n) = n3 + n 2 + n 6 +999999$ — $n3$ $O(n_3)$ 高阶的项目数
$\lim\limits{n \to \infty} = \frac{T(n)}{f{(n)}} = T = O(f(n)) = T_{(n)}$
==当我们遇到问题规模很大的时候,我们完全可以只考虑最高阶的项目数==
==并且可以去掉常数项==
4.2 空间复杂度
4.2.1内存空间固定
void loveYou(int n)
{
int i = 1;
while(i<=n)
{
i++;
printf("I Love You %d /n" , i);
}
printf("I Love You More Than %d\n" , n);
}
int main()
{
loveYou(3000);
}
S(n) = 4 + 4
内存空间所占空间大小固定 空间复杂度 $S(n) = O(1)$
该算法空间和问题复杂度无关
4.2.2 空间和复杂度有关系
下面这个程序的问题复杂度就和空间有关系了
void test(int n)
{
int in[n];
int i;
}
占用空间
4 + 4n + 4
$S{(n)} = 4 + 4n + 4$ === $S(N) = 4n$ == $S{(N)} = O_{(N)}$
$\lim\limits{n \to \infty} = \frac{S{(n)}}{f{(n)}} = T = O(f{(n)}) = T_{(n)}$
空间复杂度 $S(n) = O(n)$
void test(int n)
{
int in[n][n];
int i;
}
占用空间
4 + 4n^2 + 4
空间复杂度 $S(n) = O(n^2)$
第二章 线性表

一、线性表的类型定义
线性表是具有 ==相同==数据类型的 n 个==数据元素== 的有限序列 ,其n 为表长, 当 n = 0 时 线性表时一个空表 ,若L命令线性表,则其一般表示为 $L = (a_0 , a_1 , … ,a_i,a_{i+1} , a_n)$
$a_i$ 是线性表中的第i 个元素 是线性表中的==位序==
==位序 index== : 从 0 开始计算
==数据个数 len== : 从 1 开始计算
$a_1$ 是表头元素
特性 : 线性表是具有唯一前驱 和唯一后继 ,表头没有前驱 表尾没有后继 (双向循环链表除外)
二、顺序表的抽象数据类型
第三章 顺序表
一、顺序表的抽象数据类型
线性表的==顺序存储==又称为顺序表,用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在存储中也相邻。
==逻辑结构== 线性结构 -> 顺序表
==存储结构== 顺序存储 -> 数组
1.1 数据对象
// 数据对象
typedef struct Elenemt_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Elenemt_data;
1.2 数据关系
// 数据关系
typedef struct
{
Elenemt_data * data; // 顺序表的动态分配
int max; // 存储顺序表的最大空间
int len; // 存储有效数据的个数
}Sql_list;
1.3 基本操作
顺序表的创建:Init_Sql_List
顺序表的插入:tail_insert_tail pos_insert_list
顺序表的删除:tail_del_list pos_del_list
顺序表的查找:find_by_index find_by_value
顺序表的遍历:printf_Sql_List
顺序表的判空:IsEmpty_Sql_List
顺序表的清空:Clear_Sql_List
顺序表的合并:Merge_Sql_Lists
顺序表的扩容:Expand_Sql_List
顺序表的销毁:Destroy_Sql_List
二、 动态 & 静态 顺序表
2.1 顺序表实现 静态分配
// 数据对象
typedef struct Elenemt_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Elenemt_data;
// 数据关系
typedef struct
{
Stu_t S[128]; // 顺序表的静态分配
// 在空间是连续的
// 在逻辑是连续的
int len; // 有效数据 的个数
}Sql_list;
// 初始化
void init(Sql_list *L)
{
L.len = 0;
}
2.2 顺序表实现 动态分配
#include <stdio.h>
#include <stdlib.h>
// 数据对象
typedef struct Element_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年龄
int id; // 学号
int sco; // 成绩
} Element_data;
// 数据关系
typedef struct
{
Element_data *data; // 顺序表的动态分配
int max; // 存储顺序表的最大空间
int len; // 存储有效数据的个数
} Sql_list;
// 初始化操作
// 需要输入初始最大空间大小
Sql_list *init_list(int MAX_SIZE)
{
// 为数据关系结构体创建一个动态空间
Sql_list *L = (Sql_list *)malloc(sizeof(Sql_list));
if (L == NULL)
{
printf("分配内存失败\n");
return NULL;
}
// 为数据对象创建一个动态空间
L->data = (Element_data *)malloc(MAX_SIZE * sizeof(Element_data));
if (L->data == NULL)
{
printf("分配内存失败\n");
free(L);
return NULL;
}
// 初始化 max 和 len
L->max = MAX_SIZE;
L->len = 0;
// 返回数据关系结构体
return L;
}
// 扩容操作
void Expand_Sql_List(Sql_list *L, int num)
{
// 安全检查
if (L == NULL || L->data == NULL)
{
printf("顺序表无效\n");
return;
}
if (num < L->max)
{
printf("新容量小于当前最大容量\n");
return;
}
// 创建新空间,大小为参数 num
Element_data *p = L->data;
L->data = (Element_data *)malloc(num * sizeof(Element_data));
if (L->data == NULL)
{
printf("分配内存失败\n");
return;
}
// 拷贝数据
for (int i = 0; i < L->len; i++)
{
L->data[i] = p[i];
}
// 改写 max 值
L->max = num;
// 释放原始空间
free(p);
}
int main()
{
// 初始化顺序表
Sql_list *L = init_list(128);
if (L == NULL)
{
printf("初始化顺序表失败\n");
return 1;
}
printf("L->data = %p\n", (void *)L->data);
// 扩容顺序表
Expand_Sql_List(L, 256);
printf("L->data = %p\n", (void *)L->data);
printf("L->max = %d\n", L->max);
// 释放内存
free(L->data);
free(L);
return 0;
}
2.3 二级指针专题
首先考虑一个问题
二级指针 解引用 一次 是什么 ==得到的是一级指针==
二级指针 解引用 两次 是什么 ==指针指向 变量 的值==
在前面的声明空间中,我们所传入的内存不是堆空间内存
在我们这里将Sql_list *L 直接传入的方式 是有问题的如下
内存
void init_list(Sql_list *L)
Sql_list *L
init_list(L);
这种方式是错误的
Sql_list *L 8 字节
void init_list(Sql_list *L)
L->s 赋值
L->len 赋值 // 段错误
L->max 赋值 // 段错误
错误原因 如果下次遇到这种问题,我们可以思考是不是传入了一级指针 并且一级指针没有指向
Sql_list * init_list(void)
{
sql_list * L = malloc(大小);
L->s = malloc(大小)
L->max = 0;
L->len = 0;
return L;
}
// 需要进行两次释放
// free(L->s)
// L->s = NULL;
// free(L)
// L = NULL
因为在这里 L 并没有一个明确的指向,所以内部没有一个可以操作的数据。
说会二级指针,二级指针其实并没有什么难得,我们只需要搞明白,二级指针解引用后得到得是什么,二级指针取地址取得是谁的地址。

此外,我们还需要考虑一个问题,在上述问题中能不能不用二级指针 ==可以==
方案有三
初始条件
void init_list(Sql_list **L)
//方案一 传入的 L 先进行 一次 malloc
Sql_list * L = (Sql_list *)malloc(sizeof(Sql_list));
//方案二 传入的数据为 L 而不是 指针L
Sql_list L;
init_list(&L) 通过取地址的方式传递
//方案三 传入的数据为 指针L 但是已经提前指向了一个结构体
Sql_list data;
Sql_list * L = &data;
init_list(L);
二、顺序表的基本操作
2.1 顺序表的创建
2.1.1 思路
1、创建动态空间。
2、判断动态空间是否创建成功。
3、将顺序表的长度 len 和最大容量 max 初始化为 0。
2.1.2 示例代码
// 初始化操作
// 需要输入初始最大空间大小
Sql_list *init_list(int MAX_SIZE)
{
// 为数据关系结构体创建一个动态空间
Sql_list *L = (Sql_list *)malloc(sizeof(Sql_list));
if (L == NULL)
{
printf("分配内存失败\n");
return NULL;
}
// 为数据对象创建一个动态空间
L->data = (Element_data *)malloc(MAX_SIZE * sizeof(Element_data));
if (L->data == NULL)
{
printf("分配内存失败\n");
free(L);
return NULL;
}
// 初始化 max 和 len
L->max = MAX_SIZE;
L->len = 0;
// 返回数据关系结构体
return L;
}

==我们在编写 if (L == NULL) 语句的时候 很容易出现 写成L=NULL 的问题,所以我们需要养成一个习惯,在编写这种语句的时候,将常量写在变量的前面,例如可以写成 if(NULL == L)==
2.2 顺序表的插入
2.2.1 思路
尾插思路
int tail_insert_tail(Sql_list *L, Stu_t data)
进行安全判断:
判断顺序表是否存在。
判断顺序表是否已满。
将数据插入到顺序表的末尾。
更新顺序表的长度。

任意位置插入思路
int pos_insert_list(Sql_list *L, int index, Stu_t data)
进行安全判断:
判断顺序表是否存在。
判断插入位置是否合法。
判断顺序表是否已满。
将插入位置后的数据往后移动一位。
插入数据。
更新顺序表的长度

2.2.2 示例代码
尾插示例代码
int tail_insert_tail(Sql_list *L, Element_data data) {
// 1. 安全判断
if (L == NULL) {
printf("顺序表不存在\n");
return -1; // 表示失败
}
if (L->len >= L->max) {
printf("顺序表已满,无法插入\n");
return -1; // 表示失败
}
// 2. 插入数据,尾插
L->data[L->len] = data;
// 3. 进行 len 迭代
L->len++;
return 0; // 表示成功
}
任意位置插入
int pos_insert_list(Sql_list *L, int index, Element_data data)
{
// 安全检查
if (NULL == L)
{
printf("表不存在\n");
return -1;
}
if (L->len >= L->max)
{
printf("表已满\n");
return -1;
}
if (index < 0 || index > L->len)
{
printf("插入位置非法\n");
return -1;
}
// 开始移动
for (int i = L->len; i > index; i--)
{
L->data[i] = L->data[i - 1];
}
// 开始插入
L->data[index] = data;
L->len++;
return 0;
}
2.3 顺序表的删除
2.3.1 思路
尾删思路
int tail_del_list(Sql_list *L, int index, Element_data *data);
1. 安全检查
- 判断顺序表是否存在。
- 判断顺序表是否为空。
2. 将要删除的内容赋值给返回元素 data
3. 删除元素
- 将最后一个元素赋值给返回元素 data
- 减少顺序表的长度(len--)
任意位置删除
int pos_del_list(Sql_list *L, int index, Element_data *data);
1. 安全检查
- 判断顺序表是否存在。
- 判断删除位置是否合法。
- 判断顺序表是否为空。
2. 将要删除的内容赋值给返回元素 data
3. 对当前位置后面的数据依次往前移动
4. 更新顺序表的长度(len--)

2.3.2 代码实例
尾删
int tail_del_list(Sql_list *L, int index, Element_data *data) {
// 1. 安全检查
if (L == NULL) {
printf("顺序表不存在\n");
return -1;
}
if (L->len <= 0) {
printf("顺序表为空,无法删除\n");
return -1;
}
// 2. 将要删除的元素赋值给返回元素 data
*data = L->data[L->len - 1];
// 3. 删除元素
L->len--;
return 0; // 返回成功
}
任意位置删
int pos_del_list(Sql_list *L, int index, Element_data *data) {
// 1. 安全检查
if (L == NULL) {
printf("顺序表不存在\n");
return -1;
}
if (index < 0 || index >= L->len) {
printf("删除位置不合法\n");
return -1;
}
if (L->len <= 0) {
printf("顺序表为空,无法删除\n");
return -1;
}
// 2. 将要删除的内容赋值给返回元素 data
*data = L->data[index];
// 3. 对当前位置后面的数据依次往前移动
for (int i = index; i < L->len - 1; i++) {
L->data[i] = L->data[i + 1];
}
// 4. 更新 len
L->len--;
return 0; // 返回成功
}
2.4 顺序表的查找
2.4.1 思路
按位置查找
进行安全检查,确保顺序表存在且查找位置合法。
获取指定位置的数据。
按值查找
进行安全检查,确保顺序表存在。
遍历顺序表,查找与目标值匹配的元素。
如果找到,返回该元素的索引;如果未找到,返回 -1。
2.4.2 代码实例
按位置查找
// 按位置查找
int find_by_index(Sql_list *L, int index, Element_data *data) {
// 1. 安全判断
if (L == NULL) {
printf("顺序表不存在\n");
return -1;
}
if (index < 0 || index >= L->len) {
printf("查找位置不合法\n");
return -1;
}
// 2. 获取数据
*data = L->data[index];
return 0; // 返回成功
}
按值查找
// 按值查找
int find_by_value(Sql_list *L, Element_data value, int *index) {
// 1. 安全判断
if (L == NULL) {
printf("顺序表不存在\n");
return -1;
}
// 2. 遍历查找
for (int i = 0; i < L->len; i++) {
if (L->data[i].id == value.id) {
*index = i;
return 0; // 找到
}
}
// 未找到
*index = -1;
return -1;
}
2.5 顺序表的遍历
2.5.1 思路
安全判断:确保顺序表不为空,避免出现空指针异常。
遍历顺序表:使用循环逐个访问顺序表中的每个元素。
打印元素信息:对每个元素,打印其包含的姓名、性别、年龄、学号和成绩等信息。
2.5.2 示例代码
// 遍历打印
void printf_Sql_List(Sql_list * L)
{
// 1. 安全判断
if (L == NULL) {
printf("顺序表不存在\n");
return;
}
for (int i = 0; i < L->len; i++)
{
printf("姓名 :%s\t" , L->S[i].name);
printf("性别 :%s\t" , L->S[i].sex);
printf("年龄 :%d\t" , L->S[i].age);
printf("学号 :%d\t" , L->S[i].id);
printf("成绩 :%d\n" , L->S[i].sco);
}
}
2.6 顺序表的判空
2.6.1 思路
顺序表的判空操作用于检查顺序表中是否包含任何元素。判空操作通常在对顺序表执行其他操作之前进行,以确保顺序表中存在有效的数据。
1. 安全检查:确认顺序表是否存在,避免空指针异常。
2. 判断长度:检查顺序表的长度是否为0,如果是,则顺序表为空;否则,顺序表不为空。
2.6.2 示例代码
#include <stdbool.h>
// 判断顺序表是否为空
bool IsEmpty_Sql_List(Sql_list *L) {
// 1. 安全检查
if (L == NULL) {
printf("顺序表不存在\n");
return false; // 返回假,表示异常状态
}
// 2. 判断长度
if (L->len == 0) {
printf("顺序表为空\n");
return true; // 返回真,表示顺序表为空
} else {
printf("顺序表不为空\n");
return false; // 返回假,表示顺序表不为空
}
}
这段代码首先检查顺序表是否存在,如果顺序表为空,则返回相应的状态码,否则返回相反的状态码。
2.7 顺序表的清空
2.7.1 思路
遍历顺序表,释放顺序表中的每个数据元素。
将顺序表的长度置为零。
2.7.2 示例代码
// 清空顺序表
void Clear_Sql_List(Sql_list *L) {
if (L == NULL) {
printf("顺序表不存在\n");
return;
}
// 释放数据对象数组的内存
free(L->data);
// 重置顺序表的长度为0
L->len = 0;
}
2.8 顺序表的合并
2.8.1 思路
创建一个新的顺序表用于存储合并后的数据。
将第一个顺序表的数据复制到新的顺序表中。
将第二个顺序表的数据逐个追加到新的顺序表的末尾。
返回合并后的顺序表。
2.8.2 示例代码
// 合并两个顺序表
Sql_list* Merge_Sql_Lists(Sql_list *L1, Sql_list *L2) {
if (L1 == NULL || L2 == NULL) {
printf("顺序表不存在\n");
return NULL;
}
// 创建一个新的顺序表用于存储合并后的数据
int total_len = L1->len + L2->len;
Sql_list *merged_list = init_list(total_len);
if (merged_list == NULL) {
printf("创建顺序表失败\n");
return NULL;
}
// 将第一个顺序表的数据复制到新的顺序表中
for (int i = 0; i < L1->len; ++i) {
merged_list->data[i] = L1->data[i];
}
merged_list->len = L1->len;
// 将第二个顺序表的数据逐个追加到新的顺序表的末尾
for (int j = 0; j < L2->len; ++j) {
merged_list->data[merged_list->len++] = L2->data[j];
}
return merged_list;
}
2.9 顺序表的扩容
2.9.1 思路
安全检查:检查顺序表及其数据是否有效。
判断是否需要扩容:判断新容量是否大于当前最大容量。
创建新空间:根据扩容需求创建新的动态空间。
拷贝数据:将原顺序表中的数据复制到新的空间中。
更新最大容量:将顺序表的最大容量更新为新容量。
释放原始空间:释放原始的动态空间。
2.9.2 示例代码
// 扩容操作
void Expand_Sql_List(Sql_list *L, int num) {
// 安全检查
if (L == NULL || L->data == NULL) {
printf("顺序表无效\n");
return;
}
if (num <= L->max) {
printf("新容量小于等于当前最大容量,无需扩容\n");
return;
}
// 创建新空间,大小为参数 num
Element_data *new_data = (Element_data *)malloc(num * sizeof(Element_data));
if (new_data == NULL) {
printf("分配内存失败\n");
return;
}
// 拷贝数据
for (int i = 0; i < L->len; i++) {
new_data[i] = L->data[i];
}
// 释放原始空间
free(L->data);
// 更新顺序表信息
L->data = new_data;
L->max = num;
}
2.10 顺序表的销毁
2.10.1 思路
安全检查:确保顺序表及其数据对象的有效性。
释放数据空间:释放顺序表中存储数据的动态分配空间。
释放顺序表空间:释放顺序表的动态分配空间。
将顺序表指针置为 NULL,避免野指针的产生。
2.10.2 示例代码
// 顺序表的销毁
void Destroy_Sql_List(Sql_list **L) {
// 安全检查
if (L == NULL || *L == NULL) {
printf("顺序表无效\n");
return;
}
// 释放数据空间
free((*L)->data);
// 释放顺序表空间
free(*L);
// 将顺序表指针置为 NULL
*L = NULL;
}
第四章 链表
一、链表的定义
链表是由一系列节点组成,每个节点包含==数据==和==指向==下一个节点的地址。链表中的节点可以动态地分配内存空间,不像数组需要预先分配固定大小的空间。链表可以分为==单向链表==和==双向链表== ==循环链表== ==双向循环链表== 四种形式。
单向链表中,每个节点包含指向下一个节点的指针,最后一个节点的指针指向 NULL,表示链表的结束。双向链表中,每个节点不仅包含指向下一个节点的指针,还包含指向前一个节点的指针,这样可以从任意一个节点开始遍历链表。
==数据域==
==指针域==

表示形式
// 数据对象
typedef struct
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Stu_t;
// 节点结构体
typedef struct Node
{
Stu_t data; // 数据域 用于存储当前节点的数据
struct Node * next; // 指针域 指向下一个节点
}Node;
// 头节点定义
typedef struct Link_list
{
Node * head;
}Link_list;
1.1 头指针和头节点的概念
- 头指针:指向链表第一个节点的指针,是链表的入口。
- 头节点:位于链表开始处的额外节点,不存储数据,用于标识链表的起始位置。
==当没有头节点的时候,头指针就是第一个节点==
1.2 带头节点和不带头节点
- 带头节点:链表的第一个节点不存储数据,仅用于标识链表的起始位置,操作统一简洁。
- 空表判断 L->next== NULL;
- 不带头节点:链表的第一个节点存储数据,操作需要额外条件判断,相对复杂。
- 空表判断 L == NULL;
1.3 带头节点的两种表现形式
1.3.1 用本身来做头节点
// 节点结构体
typedef struct Node
{
Stu_t data; // 数据域 用于存储当前节点的数据
struct Node * next; // 指针域 指向下一个节点
}Node;
头节点 不使用也不存储 数据 只使用指针域
Node->next 去指向第一个元素
1.3.2 定义一个结构体来做头节点
// 头节点定义
typedef struct Link_list
{
Node * head;
}Link_list;
头节点 没有数据域
Link_list->head 去指向第一个元素
二、单向链表
2.1 单链表抽象数据类型
2.1.1 数据对象
// 数据对象
typedef struct {
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
} Stu_t;
2.2.2 数据关系
// 节点结构体
typedef struct Node {
Stu_t data; // 数据域 用于存储当前节点的数据
struct Node* next; // 指针域 指向下一个节点
} Node;
```c
// 头节点定义
typedef struct Link_list {
Node* head;
} Link_list;
2.2.3 基本操作
// 单链表的创建
Link_list* init_link_list();
// 单链表的插入
void insert_node(Link_list* list, Stu_t data, int index);
// 单链表的删除
void delete_node(Link_list* list, int id);
// 单链表的查找
Node* find_node_id(Link_list* list, int id);
Node* find_node_name(Link_list* list, char* name);
// 单链表的遍历
void print_link_list(Link_list* list);
// 单链表的判空
int IsEmpty_Sql_List(Link_list* list);
// 单链表的清空
void clear_link_list(Link_list* list);
// 单链表的合并
Link_list* merge_link_lists(Link_list* list1, Link_list* list2);
// 单链表的销毁
void free_link_list(Link_list* list);
2.2 单链表的创建
2.2.1 思路
1. 创建头节点
2. 判断是否成功,如果成功则将头节点的头指针指向null 并返回头节点的地址
3. 创建失败返回NULL

2.2.2 示例代码
// 链表的创建
Link_list* init_ink_List()
{
// 创建头节点
Link_list * L = (Link_list * )malloc(sizeof(Link_list));
// 判断是否创建成功
if (NULL != L)
{
//如果成功则初始化链表中的头节点为 NULL
L->head = NULL;
}
else
{
printf("创建失败\n");
return NULL;
}
// 返回链表结构体
return L;
}
2.3 单链表的插入
2.3.1 思路
创建新节点,并将数据写入节点中。
判断是否为第一个元素:
- 如果是在头部,则将新节点的 next 指针指向头节点next,然后将头节点next指向新节点。
开始遍历,找到要插入位置的前一个元素:
- 使用循环遍历链表,直到找到插入位置的前一个节点。
如果遍历到NULL位置,则越界,插入失败。
将新节点的 next 指针指向原插入位置的next,将前一个节点的 next 指针指向新节点。
- 头插法 动图

- 尾插法 动图

- 任意位置插入 动图

- 头插思路 图片

- 任意位置插入思路 图片

2.3.2 代码实例
// 链表的插入操作
void insert_node(Link_list* list, Stu_t data, int position) {
// 创建新节点,并将数据写入到节点中
Node* new_node = (Node*)malloc(sizeof(Node));
if (new_node == NULL) {
printf("创建新节点失败\n");
return;
}
new_node->data = data;
new_node->next = NULL;
// 判断是否为第一个元素或者链表为空
if (position == 0 || list->head == NULL) {
// 如果是在头部,则将新节点的指针指向当前头节点,再将头节点指向新节点
new_node->next = list->head;
list->head = new_node;
return;
}
// 开始遍历,找到要插入位置的前一个元素
Node* current = list->head;
for (int i = 0; i < position - 1 && current != NULL; i++) {
current = current->next; // 遍历下一个节点
}
// 已经遍历到NULL位置,即位置越界
if (current == NULL) {
printf("插入位置越界\n");
free(new_node); // 释放新节点的内存
return;
}
// 将新节点的next指针指向原插入位置的节点,将前一个节点的next指针指向新节点
new_node->next = current->next;
current->next = new_node;
}
2.4 单链表的删除
2.4.1 思路
安全检查:
- 检查链表是否存在。
创建两个新节点 p 和 q:
- p 指向要删除的前一个节点。
- q 指向要删除的节点。
遍历链表,找到要删除节点的前一个节点 p:
- 使用循环遍历链表,直到找到要删除的节点的前一个节点。
将 p 的下一个节点指针指向 q 的下一个节点:
- 通过修改 p 节点的 next 指针,将其指向 q 节点的下一个节点,跳过要删除的节点。
释放要删除的节点的内存空间:
- 使用 free() 函数释放要删除节点的内存空间。
- 单链表的删除 动图


2.4.2 代码
// 链表的删除操作
void delete_node(Link_list* list, int index) {
// 安全检查
if (list == NULL) {
printf("链表不存在\n");
return;
}
// 如果要删除的是头节点
if (index == 0) {
// 如果链表为空,则直接返回
if (list->head == NULL) {
printf("链表为空,无法删除\n");
return;
}
Node* temp = list->head; // 保存头节点的位置
list->head = list->head->next; // 将头指针指向下一个节点
free(temp); // 释放原头节点的内存空间
return;
}
// 任意位置删除
// 创建两个节点指针 p 和 q,p指向要删除节点的前一个节点,q指向要删除的节点
Node* p = list->head;
Node* q = NULL;
// 遍历链表,找到要删除节点的前一个节点 p
for (int i = 0; i < index - 1 && p != NULL; i++) {
p = p->next;
}
// 如果找不到要删除的节点,或者要删除的节点已经是最后一个节点,则提示错误并返回
if (p == NULL || p->next == NULL) {
printf("要删除的节点不存在\n");
return;
}
q = p->next; // 将 q 指向要删除的节点
p->next = q->next; // 将 p 的 next 指针指向 q 的下一个节点
free(q); // 释放要删除的节点的内存空间
return ;
}
2.5 单链表的查找
2.5.1 思路
按位置查找
单链表按位置查找操作需要按照以下步骤进行:
1. 安全判断:判断链表是否存在,以及给定的位置是否合法。
2. 获取数据:从链表的头节点开始,依次移动指针,直到找到目标位置的节点。
3. 返回目标位置的节点数据。
按值查找
单链表按值查找操作需要按照以下步骤进行:
1. 安全判断:判断链表是否存在,以及给定的值是否合法。
2. 遍历查找:从链表的头节点开始,依次移动指针,直到找到目标值的节点。
3. 如果找到目标值,返回节点的位置;否则,返回未找到的标志。
动图

2.5.3 示例代码
按位置找
// 按位置查找节点
Node* find_node_index(Link_list* list, int index) {
// 安全检查
if (list == NULL) {
printf("链表不存在\n");
return NULL;
}
// 如果要查找的位置小于0,或者链表为空,则直接返回 NULL
if (index < 0 || list->head == NULL) {
printf("链表为空或位置不合法\n");
return NULL;
}
// 创建一个指针用于遍历链表
Node* current = list->head;
// 遍历链表,找到指定位置的节点
for (int i = 0; i < index; i++) {
// 如果链表遍历到尽头还未找到指定位置的节点,则返回 NULL
if (current->next == NULL) {
printf("指定位置不存在节点\n");
return NULL;
}
// 否则,继续向后移动指针
current = current->next;
}
// 返回找到的节点指针
return current;
}
按值(按名字)找
// 按位置查找节点
Node* find_node_name(Link_list* list, char* name) {
// 安全检查
if (list == NULL) {
printf("链表不存在\n");
return NULL;
}
// 如果要查找的位置小于0,或者链表为空,则直接返回 NULL
if (index < 0 || list->head == NULL) {
printf("链表为空或位置不合法\n");
return NULL;
}
// 创建一个指针用于遍历链表
Node* current = list->head;
// 遍历链表,找到指定位置的节点
for (int i = 0; i < index; i++) {
// 如果链表遍历到尽头还未找到指定位置的节点,则返回 NULL
if (current->next == NULL) {
printf("指定位置不存在节点\n");
return NULL;
}
if (!strcmp(name , current->data.name) )
{
return current;
}
// 否则,继续向后移动指针
current = current->next;
}
// 返回找到的节点指针
printf("没找到\n");
return NULL;
}
2.6 单链表的遍历
2.6.1 思路
主要的思路为对整个链表进行遍历然后对每个节点的数据进行打印
操作步骤如下:
1、从链表的头节点开始,依次访问每个节点。
p = p.next
2、对于每个节点,访问节点中存储的数据,并进行相应的操作。
3、将访问指针指向下一个节点,直到链表的末尾(即指针为 NULL)。
2.6.2 示例代码
// 单链表的遍历
void print_Link_List(Link_list *list) {
// 安全检查
if (list == NULL) {
printf("链表不存在\n");
return;
}
// 如果链表为空,则直接返回
if (list->head == NULL) {
printf("链表为空\n");
return;
}
// 创建一个指针用于遍历链表
Node* current = list->head;
// 遍历链表并打印节点数据
while (current != NULL) {
printf("姓名: %s\t", current->data.name);
printf("性别: %s\t", current->data.sex);
printf("年龄: %d\t", current->data.age);
printf("学号: %d\t", current->data.id);
printf("成绩: %d\n", current->data.sco);
// 将指针移到下一个节点
current = current->next;
}
}
2.7 单链表的判空
2.7.1 思路
单链表的判空操作需要进行以下步骤:
判断链表是否存在,即链表指针是否为 NULL。
判断链表是否为空,即链表是否有头节点。如果链表的头节点为空,则认为链表为空。
在前面讲过,我们的链表有头节点的时候 可以通过 list->head == NULL 来判断是否为空
2.7.2 示例代码
// 单链表的判空
int is_empty_link_list(Link_list* list) {
// 安全检查
if (list == NULL) {
printf("链表不存在\n");
return -1; // 链表不存在
}
// 如果链表的头节点为空,则认为链表为空
if (list->head == NULL) {
printf("链表为空\n");
return 1; // 链表为空
}
return 0; // 链表不为空
}
2.8 单链表的清空
2.8.1 思路
单链表的清空操作需要按照以下步骤进行:
初始化两个指针变量,一个指向当前节点(N),一个指向临时节点(temp)。
开始遍历链表,将当前节点指针指向链表的头节点。
在循环中,逐个释放节点的内存空间:
a. 将临时节点指针(temp)指向当前节点(N)。
b. 将当前节点指针(N)指向下一个节点。
c. 释放临时节点指向的内存空间。
循环直到当前节点指针(N)指向 NULL,即链表末尾。
2.8.2 示例代码
// 单链表的清空
void clear_link_list(Link_list* list)
{
// 1. 初始化指针变量
Node *N = list->head;
Node *temp = NULL;
// 2. 开始遍历
while (N != NULL)
{
// 3. 释放节点的内存空间
temp = N; // a. 将临时节点指针指向当前节点
N = N->next; // b. 将当前节点指针指向下一个节点
free(temp); // c. 释放临时节点的内存空间
}
// 4. 重置链表头节点指针
list->head = NULL;
}
2.9 单链表的合并
2.9.1 思路
创建一个新的单链表,用于存储合并后的结果。
遍历第一个链表,将其中的节点逐个复制到新链表中。
遍历第二个链表,将其中的节点逐个复制到新链表中。
返回合并后的链表。
如果合并之后 两个表不要了 就直接释放 free_link_list(list1) free_link_list(list2)
2.9.2 示例代码
// 单链表的合并
Link_list* merge_link_lists(Link_list* list1, Link_list* list2) {
// 创建新的单链表用于存储合并后的结果
Link_list* New_list = init_ink_List();
if ( NULL == New_list ) {
printf("创建新链表失败\n");
return NULL;
}
// 遍历第一个链表,将节点逐个复制到新链表中
Node* temp = list1->head;
while (temp != NULL) {
Insert_Node(New_list, temp->data, New_list->len);
temp = temp->next;
}
// 遍历第二个链表,将节点逐个复制到新链表中
temp = list2->head;
while (temp != NULL) {
Insert_Node(New_list, temp->data, New_list->len);
temp = temp->next;
}
return New_list;
}
2.10 单链表的销毁
2.10.1 思路
单链表的销毁需要释放链表中的所有节点以及链表本身的内存空间。
可以通过遍历链表,依次释放每个节点的内存空间,并最后释放链表结构体的内存空间来实现。
单链表的销毁需要按照以下步骤进行:
1. 初始化两个指针变量,一个指向当前节点(N),一个指向临时节点(temp)。
2. 开始遍历链表,将当前节点指针指向链表的头节点。
3. 在循环中,逐个释放节点的内存空间:
a. 将临时节点指针(temp)指向当前节点(N)。
b. 将当前节点指针(N)指向下一个节点。
c. 释放临时节点指向的内存空间。
4. 循环直到当前节点指针(N)指向 NULL,即链表末尾。
5. 释放链表结构体的内存空间。
2.10.2 示例代码
// 链表的销毁
void free_link_list(Link_list* list)
{
// 1. 初始化指针变量
Node *N = list->head;
Node *temp = NULL;
// 2. 开始遍历
while (NULL != N)
{
// 3. 释放节点的内存空间
temp = N; // a. 将临时节点指针指向当前节点
N = N->next; // b. 将当前节点指针指向下一个节点
free(temp); // c. 释放临时节点的内存空间
temp = NULL; // 重置临时节点指针
}
// 4. 释放链表结构体的内存空间
free(list);
return ;
}
三、双向链表
3.1 双向链表的抽象数据类型
3.1.1 数据对象
// 数据对象
typedef struct Elenemt_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Elenemt_data;
3.1.2 数据关系
// 定义双向链表节点结构体
typedef struct Double_Node {
Elenemt_data data; // 数据域
struct Double_Node* prev;// 指向前一个节点的指针
struct Double_Node* next;// 指向下一个节点的指针
} Double_Node;
// 定义双向链表结构体
typedef struct Double_Link_List {
Double_Node * head; // 指向链表头节点的指针
} Double_Link_List;
3.1.3 基本操作
// 双向链表的创建
Double_Link_List* init_double_link_list();
// 双向链表的插入
void insert_double_node(Double_Link_List* list, Element_data data, int index);
// 双向链表的删除
void delete_double_node(Double_Link_List* list, int index);
// 双向链表的查找
Double_Node* find_double_node_pos(Double_Link_List* list, int id);
Double_Node* find_double_node_name(Double_Link_List* list, char* name);
// 双向链表的遍历
void print_forward_double_link_list(Double_Link_List* list);
void print_backwards_double_link_list(Double_Link_List* list);
// 双向链表的判空
int is_empty_double_link_list(Double_Link_List* list);
// 双向链表的清空
void clear_double_link_list(Double_Link_List* list);
// 双向链表的合并
Double_Link_List* merge_double_link_lists(Double_Link_List* list1, Double_Link_List* list2);
// 双向链表的销毁
void free_double_link_list(Double_Link_List* list);
3.2 双向链表的创建
3.2.1 思路
分配内存空间,创建双向链表的头节点。
判断内存分配是否成功,若成功则将头节点的前驱和后继指针均指向NULL。
返回创建结果。

3.2.2 示例代码
Double_Link_List *Init_Double_Link_List(void)
{
// 为头节点创建 动态空间
list = (Double_Link_List *)malloc(sizeof(Double_Link_List));
// 判断创建是否成功
if(NULL == list)
{
return NULL;
}
// 成功则将 前驱和后继都指向NULL
list->head = NULL;
return list;
}
3.3 双向链表的插入
3.3.1 思路
后插操作
检查链表是否存在:首先需要检查传入的链表指针是否为 NULL,如果为 NULL,则无法进行插入操作,因此需要进行安全检查。
创建新节点并分配内存空间:使用 malloc 函数为新节点分配内存空间,并进行类型转换,将返回的指针赋值给新节点的指针变量。如果内存分配失败,需要进行错误处理。
初始化新节点的数据和指针:将新节点的数据域赋值为传入的数据,同时将新节点的前驱指针和后继指针都设置为 NULL,表示当前节点尚未与其他节点连接。
处理特殊情况:
如果链表为空,即头节点指针为 NULL,或者插入位置为头节点,直接将新节点作为头节点插入链表头部,并更新头节点指针即可。
如果插入位置不是头节点,需要继续执行后续步骤。
寻找插入位置的前一个节点:从头节点开始遍历链表,直到找到插入位置的前一个节点或者遍历到链表末尾。遍历的条件是要么遍历到插入位置的前一个节点,要么当前节点的下一个节点不为空。
插入新节点:
如果找到了插入位置的前一个节点,将新节点的前驱指针指向该节点,新节点的后继指针指向该节点的后继节点,同时更新该节点的后继节点的前驱指针为新节点。
最后将该节点的后继指针指向新节点,完成插入操作。
前插操作

3.3.2 示例代码
// 双向链表的插入
void insert_double_node(Double_Link_List* list, Element_data data, int index)
{
// 检查链表是否存在
if (list == NULL)
{
printf("链表不存在\n");
return ;
}
// 创建新节点并分配内存空间
Double_Node* new_node = (Double_Node*)malloc(sizeof(Double_Node));
if (new_node == NULL)
{
printf("创建失败\n");
return ;
}
// 初始化新节点的数据和指针
new_node->data = data;
new_node->prev = NULL;
new_node->next = NULL;
// 如果链表为空或插入位置为头节点
if (list->head == NULL || index == 0)
{
// 头节点指针指向新节点,新节点的 next 指向原头节点
new_node->next = list->head;
if (list->head != NULL)
{
list->head->prev = new_node;
}
list->head = new_node;
return ;
}
// 寻找插入位置的前一个节点
Double_Node* p = list->head;
for (int i = 0; i < index - 1 && p->next != NULL; i++)
{
p = p->next;
}
// 如果找到了插入位置的前一个节点
if (p != NULL)
{
// 新节点的 next 指向原插入位置节点,prev 指向插入位置的前一个节点
new_node->next = p->next;
if (p->next != NULL)
{
p->next->prev = new_node;
}
new_node->prev = p;
p->next = new_node;
}
}
3.4 双向链表的删除
3.4.1 思路

3.4.2 示例代码
// 双向链表的删除
void delete_double_node(Double_Link_List* list, int index , Elenemt_data * data)
{
// 如果链表不存在,打印错误信息并返回
if (NULL == list)
{
printf("链表不存在");
return ;
}
// 如果链表为空,即头节点指针为 NULL,则无法执行删除操作
if (NULL == list->head)
{
printf("链表为空,无法删除\n");
return ;
}
// 定义指针变量,p指向当前节点,q指向要删除的节点
Double_Node * p = list->head;
Double_Node * q = NULL;
// 删除头节点
if(0 == index)
{
list->head = list->head->next; // 更新头节点指针
if(NULL != list->head)
{
list->head->prev = NULL; // 如果新的头节点不为空,将其前驱指针置为 NULL
}
*data = p->data; // 获取要删除节点的数据
free(p); // 释放要删除的节点的内存空间
return ;
}
// 查找要删除节点的前一个节点
for (int i = 0 ; i < index - 1 && p->next != NULL ; i ++ )
{
p = p->next;
}
// 如果前一个节点或者要删除的节点为空,打印错误信息并返回
if(NULL == p || NULL == p->next)
{
printf("要删除的节点不存在");
return ;
}
q = p->next; // 获取要删除的节点
*data = q->data; // 获取要删除节点的数据
p->next = q->next; // 更新前一个节点的指针
if(q->next != NULL)
{
q->next->prev = p; // 如果要删除节点的下一个节点不为空,更新下一个节点的前驱指针
}
free(q); // 释放要删除的节点的内存空间
}
3.5 双向链表的查找
3.5.1 思路
双向链表的查找操作可以按照节点的位置或者节点的值进行查找。
按位置查找: 根据给定的索引位置,遍历双向链表,找到对应位置的节点。
按值查找: 根据给定的节点值,遍历双向链表,找到第一个具有该值的节点。
3.5.2 示例代码
按位置查找
// 按位置查找双向链表节点
Double_Node* find_double_node_pos(Double_Link_List* list, int index) {
// 判断链表是否为空
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return NULL;
}
// 初始化当前节点为头节点的下一个节点
Double_Node* current = list->head->next;
int count = 0;
// 遍历链表,直到找到第 index 个节点或者遍历到链表末尾
while (current != list->head && count < index) {
current = current->next;
count++;
}
// 如果找到了第 index 个节点,则返回该节点;否则返回 NULL
if (count == index && current != list->head) {
return current;
} else {
printf("未找到指定位置的节点\n");
return NULL;
}
}
按值查找
// 按值查找双向链表节点
Double_Node* find_double_node_name(Double_Link_List* list, char* name) {
// 判断链表是否为空
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return NULL;
}
// 初始化当前节点为头节点的下一个节点
Double_Node* current = list->head->next;
// 遍历链表,直到找到节点值为 name 的节点或者遍历到链表末尾
while (current != list->head) {
if (strcmp(current->data.name, name) == 0) {
// 找到节点值为 name 的节点,则返回该节点
return current;
}
current = current->next;
}
// 遍历完链表未找到节点值为 name 的节点,返回 NULL
printf("未找到值为 %s 的节点\n", name);
return NULL;
}
3.6 双向链表的遍历
3.6.1 思路
双向链表的遍历可以从头节点开始向后遍历,也可以从尾节点开始向前遍历。
向前遍历: 从头节点开始,依次访问每个节点的数据,直到遍历到尾节点。
向后遍历: 从尾节点开始,依次访问每个节点的数据,直到遍历到头节点。
3.6.2 示例代码
向前遍历
// 向前遍历双向链表
void print_forward_double_link_list(Double_Link_List* list) {
// 检查链表是否为空
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return;
}
// 从头节点的下一个节点开始遍历直到回到头节点
Double_Node* current = list->head->next;
while (current != list->head) {
// 打印当前节点的数据
printf("姓名: %s, 性别: %s, 年龄: %d, 学号: %d, 成绩: %d\n", current->data.name,
current->data.sex, current->data.age, current->data.id, current->data.sco);
// 移动到下一个节点
current = current->next;
}
}
向后遍历
// 向后遍历双向链表
void print_backwards_double_link_list(Double_Link_List* list) {
// 检查链表是否为空
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return;
}
// 从尾节点开始的前一个节点开始遍历直到回到尾节点
Double_Node* current = list->head->prev;
while (current != list->head) {
// 打印当前节点的数据
printf("姓名: %s, 性别: %s, 年龄: %d, 学号: %d, 成绩: %d\n", current->data.name,
current->data.sex, current->data.age, current->data.id, current->data.sco);
// 移动到前一个节点
current = current->prev;
}
}
3.7 双向链表的判空
3.7.1 思路
双向链表判空的思路很简单,只需检查头节点是否为空即可。如果头节点为空,说明链表中没有节点,即链表为空;否则,链表非空。
3.7.2 示例代码
// 判断双向链表是否为空
int is_empty_double_link_list(Double_Link_List* list) {
// 检查头节点是否为空
if (list->head == NULL) {
printf("链表为空\n");
return 1; // 返回1表示链表为空
} else {
printf("链表非空\n");
return 0; // 返回0表示链表非空
}
}
3.8 双向链表的清空
3.8.1 思路
清空双向链表意味着将链表中所有节点都删除,最后将头节点置为空。可以通过遍历链表,依次释放每个节点的内存空间来实现清空操作。
3.8.2 示例代码
// 清空双向链表
void clear_double_link_list(Double_Link_List* list) {
if (list == NULL || list->head == NULL) {
printf("链表为空,无需清空\n");
return;
}
Double_Node* current_node = list->head->next;
Double_Node* next_node = NULL;
// 从第一个节点开始遍历链表
while (current_node != list->head) {
next_node = current_node->next; // 保存下一个节点的指针
free(current_node); // 释放当前节点的内存空间
current_node = next_node; // 移动到下一个节点
}
// 头节点置为空
list->head->next = list->head;
list->head->prev = list->head;
printf("双向链表已清空\n");
}
3.9 双向链表的合并
3.9.1 思路
要合并两个双向链表,可以分别遍历这两个链表,然后逐个将它们的节点插入到一个新的双向链表中。在插入过程中,需要确保新链表的节点顺序与原链表的顺序一致。
3.9.2 示例代码
// 链表的合并
Double_Link_List* merge_double_link_lists(Double_Link_List* list1, Double_Link_List* list2)
{
// 安全判断
if (NULL == list1 || NULL == list2)
{
printf("空表\n");
return NULL;
}
// 创建一个新链表 头节点
Double_Link_List * list3 = init_double_link_list();
Double_Node * temp = list1->head;
int index = 0;
// 遍历第一条链表
while (temp != NULL)
{
insert_double_node( list3 , temp->data , index);
temp = temp->next;
index++;
}
temp = list2->head;
index = 0;
// 遍历第一条链表
while (temp != NULL)
{
insert_double_node( list3 , temp->data , index);
temp = temp->next;
index++;
}
return list3;
}
3.10 双向链表的销毁
3.10.1 思路
双向链表的销毁操作需要释放链表中每个节点的内存空间,并释放链表头节点的内存空间。
3.10.2 示例代码
// 双向链表的销毁
void free_double_link_list(Double_Link_List** list) {
// 安全判断
if (*list == NULL || (*list)->head == NULL) {
printf("链表为空\n");
return;
}
// 初始化指针变量
Double_Node* current_node = (*list)->head->next;
Double_Node* temp_node = NULL;
// 释放节点的内存空间
while (current_node != (*list)->head) {
temp_node = current_node;
current_node = current_node->next;
free(temp_node);
}
// 释放头节点的内存空间
free((*list)->head);
// 释放链表结构体的内存空间
free(*list);
*list = NULL;
}
四、双向循环链表
4.1 双向循环链表的抽象数据类型
4.1.1 数据对象
// 数据对象
typedef struct Elenemt_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Elenemt_data;
4.1.2 数据关系
// 定义双向链表节点结构体
typedef struct Double_Node {
Elenemt_data data; // 数据域
struct Double_Node* prev;// 指向前一个节点的指针
struct Double_Node* next;// 指向下一个节点的指针
} Double_Node;
// 定义双向链表结构体
typedef struct Double_Link_List {
Double_Node * head; // 指向链表头节点的指针
} Double_Link_List;
4.1.3 基本操作
// 双向链表的创建
Double_Link_List* init_double_link_list();
// 双向链表的插入
void insert_double_node(Double_Link_List* list, Element_data data, int index);
// 双向链表的删除
void delete_double_node(Double_Link_List* list, int index);
// 双向链表的查找
Double_Node* find_double_node_pos(Double_Link_List* list, int id);
Double_Node* find_double_node_name(Double_Link_List* list, char* name);
// 双向链表的遍历
void print_forward_double_link_list(Double_Link_List* list);
void print_backwards_double_link_list(Double_Link_List* list);
// 双向链表的判空
int is_empty_double_link_list(Double_Link_List* list);
// 双向链表的清空
void clear_double_link_list(Double_Link_List* list);
// 双向链表的合并
Double_Link_List* merge_double_link_lists(Double_Link_List* list1, Double_Link_List* list2);
// 双向链表的销毁
void free_double_link_list(Double_Link_List* list);
4.2 双向循环链表的创建
4.3.1 思路
除了正常的初始化双链表,循环双链表需要在这个基础上 将头指针的next 指向自己


4.3.2 示例代码
// 双向循环链表的创建
Double_Link_List* init_double_link_list() {
Double_Link_List* list = (Double_Link_List*)malloc(sizeof(Double_Link_List));
if (list == NULL) {
printf("内存分配失败\n");
return NULL;
}
// 创建头节点
Double_Node* head = (Double_Node*)malloc(sizeof(Double_Node));
if (head == NULL) {
printf("内存分配失败\n");
free(list);
return NULL;
}
head->prev = NULL;
head->next = NULL;
// 头节点的 prev 指向尾节点,尾节点的 next 指向头节点,形成循环
head->prev = head;
head->next = head;
list->head = head; // 头指针指向头节点
return list;
}
4.3 双向循环链表的插入
4.3.1 思路
双向循环链表的插入操作需要考虑以下几个步骤:
创建新节点并分配内存空间。
将新节点的 prev 指针指向插入位置的前一个节点,将新节点的 next 指针指向插入位置的后一个节点。
调整前一个节点和后一个节点的指针,使其分别指向新节点。
特别处理头节点的情况,确保循环的正确性。


4.3.2 示例代码
// 双向链表的插入
void insert_double_node(Double_Link_List* list, Elenemt_data data, int index)
{
if ( NULL == list )
{
printf("表不存在");
return ;
}
// 创建新节点
Double_Node * new_node = (Double_Node *) malloc(sizeof(Double_Node));
if (NULL == new_node)
{
printf("创建失败\n");
return ;
}
new_node->data = data;
// 如何表为空
// 扩展 表为空的判断 if (list->head->next == list->head)
if (list->head->next == list->head)
{
// 1、将新节点的 前驱 指向 头节点
new_node->prev = list->head;
// 2、将新节点的 后继 指向头节点 -- > (如果不是循环链表 则指向 空)
new_node->next = list->head;
// 3、将头节点的 后继 指向新节点
list->head->next = new_node;
// 4、将头节点的前驱 指向 新节点
list->head->prev = new_node;
return ;
}
// 寻找插入位置的前一个节点
Double_Node* prev_node = list->head;
for (int i = 0; i < index ; i++)
{
prev_node = prev_node->next;
// 检查插入位置是否合法 当循环以及循环到尾部
if (prev_node == list->head) {
printf("插入位置不合法\n");
free(new_node); // 释放新节点的内存空间
return;
}
}
// 开始插入
new_node->prev = prev_node;
new_node->next = prev_node->next;
prev_node->next->prev = new_node;
prev_node->next = new_node;
}
4.4 双向循环链表的删除
4.4.1 思路
判断链表是否为空,如果为空则无法执行删除操作。
找到待删除节点,并判断其是否存在于链表中。
调整待删除节点前后节点的指针,将其绕过待删除节点。
如果待删除节点是头节点,需要更新头指针的位置。
释放待删除节点的内存空间。
4.4.2 示例代码
// 双向链表的删除
void delete_double_node(Double_Link_List* list, int index)
{
// 安全判断 1、传入的list 是否为 不存在 2、当链表中为空
if (NULL == list)
{
printf("链表不存在\n");
return ;
}
if (NULL == list->head)
{
printf("表为空\n");
return ;
}
// 定义指针变量,current_node指向当前节点,prev_node指向前一个节点,next_node指向下一个节点
Double_Node* current_node = list->head;
Double_Node* prev_node = NULL;
Double_Node* next_node = NULL;
// 找到待删除节点
for (int i = 0; i < index; ++i) {
prev_node = current_node;
current_node = current_node->next;
// 如果回到了头节点,说明链表长度不够,无法删除指定位置的节点
if (current_node == list->head) {
printf("删除位置超出链表长度\n");
return;
}
}
next_node = current_node->next;
// 调整指针,绕过待删除节点
prev_node->next = next_node;
next_node->prev = prev_node;
free(current_node);
}
4.5 双向循环链表的查找
4.5.1 思路
双向循环链表的查找可以按照节点位置或节点值进行查找。
按位置查找:遍历链表,找到指定位置的节点即可。
按值查找:遍历链表,比较节点中的数据与目标值是否相等。
4.5.2 示例代码
// 按位置查找节点
Double_Node* find_double_node_pos(Double_Link_List* list, int index) {
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return NULL;
}
Double_Node* current_node = list->head;
int count = 0;
// 遍历链表,查找指定位置的节点
do {
if (count == index) {
return current_node; // 找到节点,返回该节点指针
}
current_node = current_node->next;
count++;
} while (current_node != list->head);
printf("未找到指定位置的节点\n");
return NULL;
}
// 按值查找节点
Double_Node* find_double_node_name(Double_Link_List* list, char* name) {
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return NULL;
}
Double_Node* current_node = list->head;
// 遍历链表,查找节点值与目标值相等的节点
do {
if (strcmp(current_node->data.name, name) == 0) {
return current_node; // 找到节点,返回该节点指针
}
current_node = current_node->next;
} while (current_node != list->head);
printf("未找到指定值的节点\n");
return NULL;
}
4.6 双向循环链表的遍历
4.6.1 思路
双向循环链表的遍历可以从头节点开始,沿着链表的指针依次访问每个节点,直到回到头节点为止。
4.6.2 示例代码
// 正向遍历双向循环链表
void print_forward_double_link_list(Double_Link_List* list) {
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return;
}
Double_Node* current_node = list->head->next; // 从头节点的下一个节点开始遍历
// 遍历链表
while (current_node != list->head) {
// 打印节点数据
printf("姓名: %s\n", current_node->data.name);
printf("性别: %s\n", current_node->data.sex);
printf("年龄: %d\n", current_node->data.age);
printf("学号: %d\n", current_node->data.id);
printf("成绩: %d\n", current_node->data.sco);
current_node = current_node->next; // 移动到下一个节点
}
}
// 逆向遍历双向循环链表
void print_backward_double_link_list(Double_Link_List* list) {
if (list == NULL || list->head == NULL) {
printf("链表为空\n");
return;
}
Double_Node* current_node = list->head->prev; // 从头节点的前一个节点开始遍历
// 遍历链表
while (current_node != list->head) {
// 打印节点数据
printf("姓名: %s\n", current_node->data.name);
printf("性别: %s\n", current_node->data.sex);
printf("年龄: %d\n", current_node->data.age);
printf("学号: %d\n", current_node->data.id);
printf("成绩: %d\n", current_node->data.sco);
current_node = current_node->prev; // 移动到前一个节点
}
}
4.7 双向循环链表的判空
4.7.1 思路
双向循环链表为空的条件是链表头节点为空。
4.7.2 示例代码
// 判断双向循环链表是否为空
int is_empty_double_link_list(Double_Link_List* list) {
return (list == NULL || list->head == NULL);
}
4.8 双向循环链表的清空
4.8.1 思路
双向循环链表的清空即将链表中的所有节点释放,并将头节点指针置为空。
4.8.2 示例代码
// 清空双向循环链表
void clear_double_link_list(Double_Link_List* list) {
if (list == NULL) {
printf("链表不存在\n");
return;
}
Double_Node* current = list->head;
Double_Node* temp;
// 遍历链表并释放每个节点的内存空间
do {
temp = current;
current = current->next;
free(temp);
} while (current != list->head);
// 将头节点指针置为空
list->head = NULL;
}
4.9 双向循环链表的合并
4.9.1 思路
要合并两个双向循环链表,可以将第二个链表的头节点连接到第一个链表的尾节点之后,然后更新两个链表的尾节点,确保链表仍然是循环的。
4.9.2 示例代码
// 合并双向循环链表
Double_Link_List* merge_double_link_lists(Double_Link_List* list1, Double_Link_List* list2) {
if (list1 == NULL || list1->head == NULL) {
printf("第一个链表为空\n");
return list2;
}
if (list2 == NULL || list2->head == NULL) {
printf("第二个链表为空\n");
return list1;
}
// 找到第一个链表的尾节点和第二个链表的尾节点
Double_Node* tail1 = list1->head->prev;
Double_Node* tail2 = list2->head->prev;
// 将第二个链表连接到第一个链表的尾节点之后
tail1->next = list2->head;
list2->head->prev = tail1;
// 将第一个链表的尾节点连接到第二个链表的尾节点之后
tail2->next = list1->head;
list1->head->prev = tail2;
// 更新第一个链表的头节点指针为原来的头节点
Double_Link_List* merged_list = list1;
// 释放第二个链表的头节点所占用的内存空间
free(list2);
return merged_list;
}
4.10 双向循环链表的销毁
4.10.1 思路
双向循环链表的销毁过程需要释放链表中的每个节点以及链表结构体本身的内存空间。首先通过遍历链表的方式释放每个节点的内存空间,然后释放链表结构体本身的内存空间。
4.10.2 示例代码
// 双向循环链表的销毁
void free_double_link_list(Double_Link_List* list) {
// 如果链表不存在,直接返回
if (list == NULL) {
printf("链表不存在\n");
return;
}
// 定义指针变量,p指向当前节点,q指向下一个节点
Double_Node* p = list->head->next;
Double_Node* q = NULL;
// 开始遍历链表,释放每个节点的内存空间
while (list->head != p) {
q = p; // 将临时节点指针指向当前节点
p = p->next; // 将当前节点指针指向下一个节点
free(q); // 释放临时节点的内存空间
}
free(list->head); // 释放链表结构体的头节点内存空间
free(list); // 释放链表结构体的内存空间
}
第五章 栈和队列
一、栈的定义
1.1 基本概念
==栈(stack) 是只允许在一端进行插入和删除操作的线性表==
后进先出
进栈 出栈
最后面的进来的 享有有限出栈权
受限制的线性表


重要术语:栈顶、栈底、空栈

二、栈的基本操作
2.1 栈的抽象数据类型
2.1.1 数据对象
// 数据对象
typedef struct Elenemt_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Elenemt_data;
2.1.2 数据关系
#define MAX_SIZE 10
typedef struct{
Elenemt_data data[MAX_SIZE]; // 静态数组存放栈中元素
int top; // top 栈顶指针
}SqSrack;
2.1.3 基本操作
// 栈的初始化
SqSrack * Init_Stack(void);
// 栈的进栈
void Push_Stack(SqSrack * S, Elenemt_data e);
// 栈的出栈
void Pop_Stack(SqSrack * S, Elenemt_data * e);
// 栈的读取 只读取栈顶部
void Get_Top(SqSrack * S, Elenemt_data * e);
// 栈的判空
int Is_Empty(SqSrack * S);
// 栈的清空
void Clear_Stack(SqSrack * S);
// 栈的销毁
void Destroy_Stack(SqSrack * S);
2.2 栈的创建
2.2.1 思路
栈的创建即为栈的初始化过程,首先需要分配内存空间以存储栈结构体,并初始化栈顶指针为-1,表示栈为空。
2.2.2 实例代码
// 栈的初始化
SqStack* Init_Stack() {
SqStack* stack = (SqStack*)malloc(sizeof(SqStack)); // 分配内存
if (stack == NULL) {
printf("内存分配失败,栈初始化失败\n");
exit(EXIT_FAILURE);
}
stack->top = -1; // 初始化栈顶指针为-1,表示栈为空
return stack;
}
2.3 栈的进栈
2.3.1 思路
栈的进栈操作即将元素压入栈中,首先需要检查栈是否已满,如果栈已满则无法进行进栈操作;如果栈未满,则将要压入的元素放入栈顶,并更新栈顶指针。
2.3.2 实例代码
// 栈的进栈
void Push_Stack(SqSrack * S, Elenemt_data data)
{
// 判断 栈是否存在
if (NULL == S)
{
puts("栈不存在");
return ;
}
// 判断栈是否满了
if (S->top == MAX_SIZE - 1)
{
puts("栈不存在");
return ;
}
// 进行top 指针的迭代
S->top ++ ;
// 传入数据
S->data[S->top] = data;
return ;
}
2.4 栈的出栈
2.4.1 思路
栈的出栈操作即将栈顶元素弹出,首先需要检查栈是否为空,如果栈为空则无法进行出栈操作;如果栈不为空,则将栈顶元素弹出,并更新栈顶指针。
2.4.2 实例代码
// 栈的出栈
void Pop_Stack(SqSrack * S, Elenemt_data * data)
{
// 判断 栈是否存在
if (NULL == S)
{
puts("栈不存在");
return ;
}
// 判断 栈是否为空
if (-1 == S->top)
{
puts("栈为空");
return ;
}
// 出栈操作
*data = S->data[S->top];
S->top--;
}
2.5 栈的判空
2.5.1 思路
栈的判空操作即检查栈是否为空,可以通过栈顶指针的值来判断。如果栈顶指针为-1,表示栈为空;否则,栈不为空。
2.5.2 实例代码
// 栈的判空
int Is_Empty(SqSrack * S)
{
if (-1 == S->top)
{
return 1;
}
return 0;
}
2.6 栈的清空
2.6.1 思路
栈的清空操作即将栈中所有元素清空,可以通过将栈顶指针重新设为-1来实现。
2.6.2 实例代码
// 栈的清空
void Clear_Stack(SqSrack * S )
{
S->top = -1;
}
2.7 栈的读取
2.7.1 思路
2.7.2 实例代码
// 栈的销毁
void Destroy_Stack(SqSrack * S , Elenemt_data * data )
{
*data = S->data[S->top];
}
2.8 栈的销毁
2.8.1 思路
栈的销毁操作包括释放栈结构体所占用的内存空间,以及清空栈中的数据。首先,需要释放栈中存储数据的数组内存空间,然后释放栈结构体本身所占用的内存空间。
2.8.2 实例代码
// 栈的销毁
void Destroy_Stack(SqSrack ** S)
{
free(*S);
*S = NULL;
}
三、队列的定义
队头、队尾、空队列
Queue 队列 只能在一段进行插入 另一端进行删除的线性表


四、队列的基本操作
4.1 栈的抽象数据类型
4.1.1 数据对象
// 数据对象
typedef struct Elenemt_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Elenemt_data;
4.1.2 数据关系
#define MAX_SIZE 10
typedef struct{
Elenemt_data data[MAX_SIZE]; // 静态数组存放队列中元素
int front; // 队头指针 指向队头的指针
int rear; // 队尾指针 指向队尾+1位置的指针
}SqQueue;
4.1.3 基本操作
// 队列的初始化
SqQueue * Init_Queue(void);
// 队列的入队
void Enqueue(SqQueue * Q, Element_data e);
// 队列的出队
void Dequeue(SqQueue * Q, Element_data * e);
// 队列的判空
int Is_Empty(SqQueue * Q);
// 队列的清空
void Clear_Queue(SqQueue * Q);
// 队列的销毁
void Destroy_Queue(SqQueue * Q);
```
如何让剩余的一个空间利用起来
方案一 : 增加一个int len 用于存储当前的元素个数
方案二 : 设定一个标志位 flag 当 进行删除的时候 设定flag = 1 当进行增加的时候, 设定flag 为0
front == rear && flag = 1 空表
front == rear && flag = 0 满表
计算元素个数
(对尾 + max - 队头) % max
(9 + 10 - 0) % 10 = 9
4.2 队列的创建
4.2.1 思路
队列的创建可以通过初始化一个空的队列来实现。首先需要分配内存空间给队列结构体,并将队头和队尾指针都初始化为零。
4.2.2 实例代码
// 队列的初始化
Sql_Queue * Init_Queue(void)
{
// 创建 动态空间
Sql_Queue * list = (Sql_Queue * )malloc(sizeof(Sql_Queue));
// 判断空间是否创建成功
if (NULL == list)
{
printf("栈创建失败\n");
return NULL;
}
// 设置初始值
list->front = list->rear = 0;
// 返回创建好的栈
return list;
}
4.3 队列的入队
4.3.1 思路
队列的入队操作需要将新元素添加到队列的尾部,并更新队尾指针。但是要注意队列已满的情况,如果队列已满则无法再添加新元素。
4.3.2 实例代码
// 队列的入队
void Enqueue(Sql_Queue * Q, Elenemt_data data)
{
// 判满
// if(Q->rear == Q->front && len == MAX) //判断为满
if ((Q->rear + 1) % MAX == Q->front)
{
printf("队列已经满了");
}
// 传入数据
Q->data[Q->rear] = data;
// 迭代
Q->rear = (Q->rear + 1) % MAX;
}
max = 10
队头
0
队尾
0
1
2
3
4
5
6
7
8
9
(9 + 1) % 10 = 0
(10 + 1) % 10 = 1
取模 运算
A % B
A > B ? 不可能
4.4 队列的出队
4.4.1 思路
队列的出队操作需要判断队列是否为空,如果队列为空则无法执行出队操作。如果队列不为空,则将队头元素出队,并更新队头指针。
4.4.2 实例代码
// 队列的出队
void Dequeue(Sql_Queue * Q, Elenemt_data * data)
{
// 判断为空
if (Q->front == Q->rear)
{
printf("表为空\n");
return ;
}
// 传入数据
* data = Q->data[Q->front];
// 进行迭代
Q->front = (Q->front + 1) % MAX;
}
4.5 队列的判空
4.5.1 思路
要判断队列是否为空,只需检查队头和队尾指针是否相等即可。如果它们相等,则队列为空;否则,队列不为空。
4.5.2 实例代码
// 队列的判空
int Is_Empty(Sql_Queue * Q)
{
// 判断为空
if (Q->front == Q->rear)
{
printf("表为空\n");
return 1;
}
return 0;
}
4.6 队列的清空
4.6.1 思路
队列的清空操作即将队列中所有元素清空,使队列恢复为空状态。这可以通过将队列的队头指针和队尾指针都设置为初始位置来实现。
4.6.2 实例代码
// 队列的清空
void Clear_Queue(Sql_Queue * Q)
{
Q->front = Q->rear = 0;
}
4.7 队列的查看
4.7.1 思路
队列的查看操作用于获取队列的队首元素,但不删除该元素。这个操作只需简单地访问队列的队首元素即可。
4.7.2 实例代码
// 查看队首元素
void Get_Queue(Sql_Queue * Q, Elenemt_data * data)
{
// 将队首元素赋值给 data
*data = Q->data[Q->front];
}
4.8 队列的销毁
4.8.1 思路
队列的销毁操作用于释放队列所占用的内存空间,包括队列结构体和存储元素的数组。在销毁队列之前,需要确保队列已经清空。然后释放队列结构体的内存空间,最后将队列指针置为 NULL,以避免悬空指针。
4.8.2 实例代码
// 销毁队列
void Destroy_Queue(SqQueue **Q) {
if (*Q == NULL) {
printf("队列不存在\n");
return;
}
// 清空队列
Clear_Queue(*Q);
// 释放队列结构体的内存空间
free(*Q);
*Q = NULL;
}
第六章 树和二叉树
一、树的基本概念

1.1 基本概念
首先,我们先看,什么是树 ==tree==
树:从树根生长 逐级分支

节点的名称

==根节点==:树结构中的第一个节点,没有父节点。根节点是树的起始节点,其他节点都是从根节点开始延伸的。
==分支节点==:也称为非叶子节点,除了根节点以外的其他节点,它们至少有一个子节点。
==叶子节点==:叶子节点是没有子节点的节点,它们是树结构中的末梢节点。叶子节点是树的结束节点,不再延伸分支。
==边==:树结构中连接节点的线称为边。边表示节点之间的关联关系和层次关系,从根节点开始,通过边可以到达树中的其他节点。
==空树==: 0 个节点
==非空树==:
有且仅有一个根节点
没有后继的节点称为 “叶子节点” 终端节点
有后继节点的称为 “分支节点” 非终端节点
除了根节点除外,任何一个节点都 有且仅有一个前驱
每个节点都可以有0个或多个后继
二叉树 - > 分支结点 最多拥有 2个后继
子树的概念
Linux -> 树结构 \
win -> 森林结构 C\: D\: E\: F\:

1.2 基本术语
1.2.1 节点之间关系的描述
关于这个节点之间的关系,我们可以利用家谱来进行描述,如下
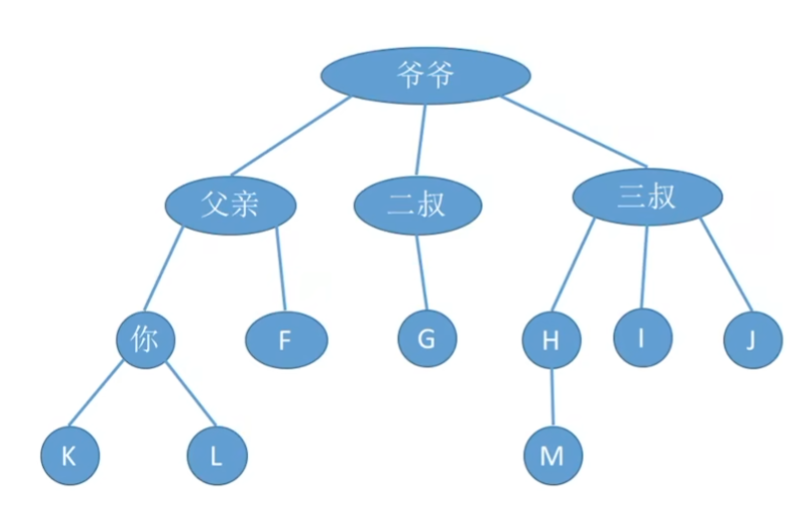
==祖先节点==:对于树中的一个节点,其祖先节点是指从根节点到该节点路径上的所有节点,不包括该节点本身。
==子孙节点==:对于树中的一个节点,其子孙节点是指以该节点为根的子树中的所有节点,包括该节点本身。
==双亲结点==:对于树中的一个节点,其双亲节点是指该节点的==父节点==。
==孩子结点==:对于树中的一个节点,其孩子节点是指直接连接到该节点下面的节点。
==兄弟结点==:对于树中的一个节点,其兄弟节点是指具有相同父节点的节点。
==堂兄弟结点==:对于树中的一个节点,其堂兄弟节点是指具有相同双亲节点但不同父节点的节点。==一般用于描述 同层节点==

==两个结点之间的路径== :两个节点之间的路径是指连接这两个节点的边的序列,其中包括这两个节点本身。
==路径长度== :路径长度是指连接两个节点之间的边的数量。
1.2.2 节点、树的属性描述
==结点的深度==:从上往下数
节点的深度是指从根节点到该节点的唯一路径上的边的数量,根节点的深度为0,其子节点的深度为1,依此类推。
==结点的高度==:从下往上数
节点的高度是指从该节点到最远叶子节点的最长路径上的边的数量,叶子节点的高度为0,根据这个定义,树的高度即为根节点的高度。
==结点的度==:节点的度是指该节点拥有的子节点(即孩子节点)的数量。==度为0 就是叶子节点==
==树的度==:树的度是指树中所有节点的度的最大值。

1.2.3 有序树、无序树
==有序树==:有序树是指树中每个节点的子节点之间有明确定义的顺序关系。
==无序树==:无序树是指树中每个节点的子节点之间没有明确的顺序关系。

1.2.4 树、森林
==linux 系统:文件系统为树状==
==Windows系统 :文件系统为森林,因为 有C\D\E==

二、树的性质
2.1 结点数
这颗树中 所有结点的个数
2.2 树的度 和 m叉树
==树的度==
一个树的度是指树中各节点的子节点数量的最大值。
==m叉树==
m叉树是一种特殊类型的树,其中每个节点最多有m个子节点。

2.3 m叉树的最多节点数问题
m叉树的最多节点数取决于树的深度和每个节点的分支度。如果 m 叉树的深度为h,根节点的分支度为m,则最多节点数为 $m^{h}-1$ (所有结点 也算根结点)。
三、二叉树的基本概念

3.1 二叉树的基本概念
在前面我们理解了m 叉树 ,那我们现在学习的二叉树 就是由一个结点和两个互不相交的 ==左子树== 和 ==右子树== 组成,左子树和右子树又分别可以分为二叉树
二叉树是一种特殊的树结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。这两个子节点也是二叉树。二叉树具有以下特点:
每个节点最多有两个子节点,分别称为左子节点和右子节点。
左子树和右子树也是二叉树,它们可以为空。
二叉树的子树之间是有序的,左子树始终在右子树之前。

==特点==:
1、每个结点最多只能有两个节点
2、左右子树不能颠倒 (二叉树是==有序树==)
3.2 二叉树的状态

3.3 特殊的二叉树
3.3.1 满二叉树
一个高度为h 且有 $2^h-1$ 个结点的二叉树
特点
1、只有一层有叶子结点
2、不存在度为1 的结点
3、按层序从1 开始编号,结点i的左孩子为$2i $右孩子 为 $2i + 1$ ,结点i 的父结点 i/2
当节点为 i 时
左孩子 2i
右孩子 2i + 1
父节点
如果节点i 为左孩子 i/2
如果节点i 为右孩子

3.3.2 完全二叉树
当树中的每个结点和满二叉树中的编号一一对应时,我们称为完全二叉树

特点:
1、只有最后两层可能有叶子结点
2、最多只有一个度为1的结点
3、和完全二叉树的特点三一样
4、如果某个结点只有一个孩子,那么这个一定是左孩子
3.3.3 二叉排序树
左子树上所有结点的关键字都小于根结点的关键子
右子树上所有结点的关键字都大于根结点的关键子
左子树和右子树又是一颗二叉排序树
==二叉排序树用于元素的搜索、排序==

3.3.4 平衡二叉树
树上的任一结点的 左子树 和 右子树的深度只差不超过1
这里的平衡二叉树所追求的平衡是为了更好的做二叉排序树

三、二叉树的存储形式
3.1 二叉树的顺序存储
3.1.1 存储的形式


3.1.2 基本操作思路
1.访问
当前结点为 i
i 的左孩子 ==2i==
i 的右孩子 ==2i+1==
i 的父结点 ==i/2==
i 所在的层次
2.判空
如果完全二叉树中共有n个结点 则
判断 i 是否有左孩子 ==2i<=n==
判断 i 是否有右孩子 ==2i+1<=n==
判断 i 是否是叶子结点 ==i>(n/2)==
3.1.3 非完全二叉树的存储形式
在前面,我们都是使用满二叉树来进行的计算,但是,如果我们现在不是满二叉树,或者说不是完全二叉树
如下


但是我们可以想办法让普通二叉树的编号和满二叉树的编号相对于


对于非完全二叉树,只能使用完全二叉树的==访问==规则 不能使用 ==判空规则==
==此外==,从上面的图中我们也可以看出来,这里是很多空间我们没有用到,但是我们也占用了,例如下图


==所以一般只用于完全二叉树和满二叉树 避免空间浪费==
3.2 二叉树的链式存储


3.2.1 数据对象
// 数据对象
typedef struct Elenemt_data
{
char name[128]; // 姓名
char sex[5]; // 性别
int age; // 年纪
int id; // 学号
int sco; // 成绩
}Elenemt_data;
3.2.2 数据关系
// 定义树节点结构体
typedef struct Tree_Node
{
Element_data data;
struct Tree_Node * lchilb; // 左孩子
struct Tree_Node * rchilb; // 右孩子
}Tree_Node;
3.2.3 基本操作
// 初始化二叉树
Tree_Node* init_binary_tree();
// 插入节点
void insert_node(Tree_Node *root, Element_data data);
// 先序遍历 根 左 右 preorder_traversal
void pre_rder(Tree_Node *root);
// 中序遍历 左 根 右 inorder_traversal
void ino_rder(Tree_Node *root);
// 后序遍历 左 右 根 postorder_traversal
void pos_rder(Tree_Node *root);
五、二叉树的遍历解析



5.1 创建二叉树
5.1.1 思路
5.1.2 实例代码
5.2 插入二叉树
5.2.1 思路
如果树为空,则创建一个新节点,并将其作为根节点。
如果树不为空,则比较要插入的数据与当前节点的数据的大小关+系:
如果要插入的数据小于当前节点的数据,则递归地将数据插入到当前节点的左子树中。
如果要插入的数据大于等于当前节点的数据,则递归地将数据插入到当前节点的右子树中。
5.2.2 实例代码
// 插入节点
void insert_node(Tree_Node **root, Element_data data) {
if (*root == NULL) {
// 如果根节点为空,则创建新节点作为根节点
Tree_Node *new_node = (Tree_Node *)malloc(sizeof(Tree_Node));
if (new_node == NULL) {
printf("创建失败\n");
return;
}
// 将数据复制到新节点的数据域中
new_node->data = data;
new_node->lchilb = NULL;
new_node->rchilb = NULL;
*root = new_node; // 将新节点作为根节点
printf("插入成功\n");
return ;
}
// 如果根节点不为空,则递归地插入到左子树或右子树中
if (data.id < (*root)->data.id) {
// 插入到左子树
insert_node(&(*root)->lchilb, data);
} else {
// 插入到右子树
insert_node(&(*root)->rchilb, data);
}
return ;
}
```
递归函数
自己调用自己
1、一定要有终止条件
5.3 先序遍历 二叉树
5.1.1 思路
若二叉树为空 则上面也不用左
若二叉树为非空
1、访问根结点
2、先序遍历左子树
3、先序遍历右子树
5.1.2 实例代码
伪代码
// 先序遍历 根 左 右
void pre_rder(Tree_Node *root)
{
if(T!=NULL)
{
// 操作
// 打印当前结点 放在这个位置 是先序遍历
pre_rder(root->lchild); // 访问左边孩子
// 打印当前结点 放在这个位置 是中序遍历
pre_rder(root->rchild); // 访问右边孩子
// 打印当前结点 放在这个位置 是后序遍历
}
}
```c
// 先序遍历 根 左 右 preorder_traversal
void pre_rder(Tree_Node *root)
{
if (root != NULL) {
// 打印当前节点的数据
printf("姓名: %s, 性别: %s, 年龄: %d, 学号: %d, 成绩: %d\n",
root->data.name, root->data.sex, root->data.age, root->data.id, root->data.sco);
// 递归遍历左子树
preorder_traversal(root->lchilb);
// 递归遍历右子树
preorder_traversal(root->rchilb);
}
}
5.4 中序遍历 二叉树
// 中序遍历 左 右 根 inorder_traversal
void ino_rder(Tree_Node *root)
{
if (root != NULL) {
// 递归遍历左子树
inorder_traversal(root->lchilb);
// 打印当前节点的数据
printf("姓名: %s, 性别: %s, 年龄: %d, 学号: %d, 成绩: %d\n",
root->data.name, root->data.sex, root->data.age, root->data.id, root->data.sco);
// 递归遍历右子树
inorder_traversal(root->rchilb);
}
}
5.5 后序遍历 二叉树
// 后序遍历 左 右 根 postorder_traversal
void pos_rder(Tree_Node *root)
{
if (root != NULL) {
// 递归遍历左子树
pos_rder(root->lchilb);
// 递归遍历右子树
pos_rder(root->rchilb);
// 打印当前节点的数据
printf("姓名: %s, 性别: %s, 年龄: %d, 学号: %d, 成绩: %d\n",
root->data.name, root->data.sex, root->data.age, root->data.id, root->data.sco);
}
}
5.6 打印节点
//打印节点用
void tree_node_print(Elenemt_data data)
{
printf("姓名 :%s\t" , data.name);
printf("性别 :%s\t" , data.sex);
printf("年龄 :%d\t" , data.age);
printf("学号 :%d\t" , data.id);
printf("成绩 :%d\n" , data.sco);
return ;
}
六、二叉树的层序遍历
6.1 思想
1、初始化一个辅助队列
2、根结点入队
3、若队列非空,则对头结点出队访问改结点 ,并将左右孩子都插入队中
4、重复三知道队列为空


第七章 排序算法
一、冒泡排序
冒泡排序是一种简单直观的排序算法,它重复地遍历要排序的列表,一次比较两个相邻的元素,并且交换它们的位置,如果它们的顺序错误就将它们交换过来。这个过程会一直重复,直到没有需要交换的元素,也就是说列表已经按照升序或降序排列完成。
1.1 算法的步骤
比较相邻的元素。如果第一个比第二个大(升序),则交换它们的位置。
对每一对相邻元素进行同样的操作,从开始第一对到结尾的最后一对。这样,在一次遍历后,最大(或最小)的元素会被交换到列表的最后一个位置。
针对所有的元素重复以上的步骤,除了最后一个。
重复步骤1~3,直到排序完成。
1.2 实例代码
// 全站内容仅供学习,禁止以原文或修改形式后的任何企业使用,请准守“一般著作权”协议
// 来源:totuma.cn
#include <stdio.h>
#include <stdlib.h>
#define ElemType int
// totuma.cn
// 冒泡排序
// 先冒最小的到最前面
void Bubble_MinToFront_Sort (ElemType A[], int n) {
int i, j, temp;
bool flag = false;
for (i = 0; i < n - 1; i++) {
flag = false;
for (j = n - 1; j > i; j--) {
// 检查相邻两个元素的大小,如果前一个大于当前,则交换它们
if (A[j - 1] > A[j]) {
temp = A[j]; // 临时变量用于交换元素
A[j] = A[j - 1];
A[j - 1] = temp;
flag = true; // 设置标志位为true,表示发生了交换
}
}
// 如果本轮没有发生交换(数组已经有序),则直接返回
if (flag == false) return;
}
}
// totuma.cn
// 冒泡排序
// 先冒最大的到最后面
void Bubble_MaxToEnd_Sort (ElemType A[], int n) {
int i, j, temp;
bool flag = false;
for (i = 0; i < n - 1; i++) {
flag = false; // 初始化标志位为false
for (j = 0; j < n - 1 - i; j++) { // 执行冒泡排序,将最大的元素冒泡到最后
// 检查相邻两个元素的大小,如果当前大于后一个,则交换它们
if (A[j] > A[j + 1]) { // 修改比较条件
temp = A[j]; // 临时变量用于交换元素
A[j] = A[j + 1]; // 将较大的元素移动到后面
A[j + 1] = temp; // 将较小的元素移动到前面
flag = true; // 设置标志位为true,表示发生了交换
}
}
// 如果本轮没有发生交换(数组已经有序),则直接返回
if (flag == false) return;
}
}
// totuma.cn
int main () {
// 注意,0号位置是哨兵,不是要排序的值
ElemType arr1[9] = {20, 60, 30, 10, 40, 90, 80, 70, 50};
Bubble_MinToFront_Sort(arr1, 9);
printf("冒泡排序(最小的往前冒)排序结果:");
for (int i = 0; i < 9; i++) {
printf("%d ", arr1[i]);
}
ElemType arr2[9] = {20, 60, 30, 10, 40, 90, 80, 70, 50};
Bubble_MaxToEnd_Sort(arr2, 9);
printf("\n冒牌排序(最大的往后冒)排序结果:");
for (int i = 0; i < 9; i++) {
printf("%d ", arr2[i]);
}
return 0;
}
1.3 算法复杂度
时间复杂度:最坏情况下为O(n^2),最好情况下为O(n)。
空间复杂度:冒泡排序是一种原地排序算法,空间复杂度为O(1)。
稳定性:冒泡排序是一种稳定的排序算法,相同元素的相对位置在排序前后不会发生变化。
二、插入排序
2.1 算法步骤

插入排序的算法步骤如下:
从第一个元素开始,该元素可以认为已经被排序。
取出下一个元素,在已经排序的元素序列中从后向前扫描。
如果该元素(已排序)大于新元素,将该元素移到下一位置。
重复步骤3,直到找到已排序的元素小于或等于新元素的位置。
将新元素插入到该位置后。
重复步骤2~5,直到整个数组排序完成。
2.2 实例代码
#include <stdio.h>
// 插入排序函数
void insertion_sort(int arr[], int n) {
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// 将大于key的元素向后移动一个位置
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// 主函数
int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr) / sizeof(arr[0]);
// 对数组进行插入排序
insertion_sort(arr, n);
// 打印排序后的数组
printf("排序后的数组:");
for (int i = 0; i < n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
return 0;
}
2.3 算法复杂度
空间复杂度 $O(1)$
时间复杂度
最好的情况 $O(n)$
最坏的情况$O(n^2)$
三、简单选择排序
5.1 算法步骤

选择排序(Selection Sort)是一种简单直观的排序算法。它的工作原理如下:
- 初始状态:将数组分为已排序区间和未排序区间。初始时,已排序区间为空,未排序区间包含所有元素。
- 选择最小元素:遍历未排序区间,找到最小的元素,将其与未排序区间的第一个元素进行交换,这样就将该元素归位到已排序区间的末尾。
- 重复操作:重复上述步骤,直到未排序区间为空,即整个数组排序完成。
5.2 实例代码
// 简单选择排序
void SelectSort(ElemType A[], int n) {
int i, j, min, temp;
// 外循环:从数组的第一个元素到倒数第二个元素进行遍历
for (i = 0; i < n - 1; i++) {
min = i; // 假设当前位置的元素是最小的
// 内循环:从外循环的下一个位置到数组末尾进行遍历
for (j = i + 1; j < n; j++) {
// 检查是否有比当前最小值更小的元素
if (A[j] < A[min])
min = j; // 如果找到更小的元素,更新最小值的索引
}
// 如果最小值的索引不等于当前位置索引,说明找到了比当前位置更小的元素
if (min != i) {
temp = A[i]; // 临时变量用于交换元素
A[i] = A[min]; // 将当前位置元素与最小值元素交换位置
A[min] = temp; // 更新最小值位置的元素为当前位置元素
}
}
}
5.3 算法复杂度
空间复杂度: $O(1)$
时间复杂度:$O(n^2)$
第八章 项目
8.1 软件开发任务背景
目前,国内航空公司的数量和规模都在扩大,国外航空公司也纷纷着陆中国,这些航 空公司之间的竞争可谓日益激烈。配备一个安全、高效、灵活、可靠的客户服务中心系统对于航空公司加强客户服务质量,提高客户服务水平,扩展业务途径,维护公众形象,提高工作效率必将发挥重要作用。基于此,要求编写一个基于航班信息管理系统的文本应用程序。
2 软件开发任务目的及意义
实现航空公司的机票销售的自动化的计算机系统,为企业的决策层提供准确、精细、迅速的机票销售信息。方便客户端进行登录,了解航班信息,购买机票等。
对国内航空公司来说,航空订票管理系统既能扩大服务范围,扩大公司影响,减少营业费用,又对稳固航空公司的客源有着重要的辅助作用;站在旅客的角度,航空公司提供的这种服务提供了更多的方便,节省了很多时间。建设航空订票管理系统是体现和提高航空公司领导业绩的一条捷径,此外还具有重要意义:
a、改善航空公司服务质量;
b、创造和提升航空公司的品牌优势;
c、优化航空公司的服务流程;
d、提升信息化的水平;
掌握基本双向循环链表等数据结构的使用和增强项目调试能力。
3 软件开发平台
- LINUX 操作系统。
- 编码工具:vscode git vim等。
- 开发语言:C语言。
4.1概述
某机场每天有n个航班,每个航班具有唯一的班次号(1、2、3…n),并且具有固定的起飞时间、固定的路线(起始站、终点站),也包含大致的飞行时间,以及固定的载客量。本系统需要设计相应的数据结构,实现对该机场航班的管理功能,需要包含添加班次、浏览班次信息、查询航班路线、购票与退票功能,其中的购票与退票操作仅可以提前十天进行。系统的数据需要在文件中进行保存,考虑到数据的维护代价、扩展性以及存取代价,本系统采用双向循环链表保存系统数据,每条航班信息通过结构体进行存储。
4.2功能分析
分等级用户登录功能:登录界面,用户名,密码。用户信息可用文件存储 , 等级分为 , 等级标识符 使用宏定义 。
增加航班信息功能:该功能实现了增加详细航班信息后,添加该信息到系统中。
浏览航班信息功能:该功能实现了将系统中所有的航班信息全部输出到屏幕上的功能。
查询航班路线功能:该功能包含两种选择,一是根据用户选择的班次信息输出对应的航班信息;二是根据用户输入的终点站,输出所有到达该站点的航班信息。(根据部分信息查询全部信息)
修改航班信息功能:该功能可以修改指定航班的某项信息,以实时更新航班信息。
删除航班信息功能:该功能实现了可以删除某项航班信息的功能。
排序航班信息功能:该功能实现了根据起飞时间进行排序功能。根据终点站首字母信息进行排序功能等。
购票功能:该功能实现了当用户指定日期与班次信息时,相应地为该航班增加售出记录,但是如果该航班已经起飞或者该航班的机票已经售空,用户将购买失败,系统会给予用户相应的提示。
退票功能:退票功能类似与购票功能,当用户指定日期与班次以后,将减少该班次的售出记录,同样的如果该班次已经起飞或者没有售出记录,则退票操作失败,系统会给予用户相应的提示。
系统所有航班信息存储在文件中功能。
其他自定义功能。

用户信息
//用户数据结构体
typedef struct user
{
char name[16]; //用户名
char passwd[64]; //用户密码
int IDcard ; //用户身份证信息
int value ; //余额
char * ticket[10]; //指针数组:存储航班信息。
}user_t;
//用户数据节点 - 单链表
typedef struct u_node
{
user_t * userm;
struct unode * next;
}u_node;
typedef struct u_list
{
struct unode * next;
}u_list;
航班信息
//航班数据结构体
typedef struct flight
{
int id; //航班班次
char flightNUM; //航班代号
char flighttype[20] ; //飞机机型
char startcity[20] ; //航班起点站
int starttime[2]; //起飞时间 时:分
char arrivecity[20] ; //航班终点站
int arrivetime[2] ; //到达时间 时:分
char flytime[20] ; //飞行时间
int value ; //票价
int maxNUM ; //额定载客量,
int leftbuyersa ; //剩余座位数量
char whetherfly ; //是否起飞 ‘y’ ‘n’
}flight_t;
//航班信息节点 - 双向循环链表
typedef struct f_node
{
void * data;
struct fnode * prev;
struct fnode * next;
}f_node;
typedef struct fnode
{
struct fnode * next;
}f_list;
文件框架
airline_system/
├── include/
│ ├── user.h // 用户相关结构体和函数声明
│ ├── flight.h // 航班相关结构体和函数声明
│ ├── list.h // 链表操作相关函数声明
│ ├── dlist.h // 双向循环链表操作相关函数声明
│ ├── array.h // 顺序表操作相关函数声明
│ └── utils.h // 公用工具函数声明
├── src/
│ ├── main.c // 主程序入口
│ ├── user.c // 用户功能实现 用户 单链表的增删改查
│ ├── flight.c // 航班功能实现 航班 双向循环链表的增删改查
│ ├── list.c // 链表操作实现
│ ├── dlist.c // 双向循环链表操作实现
│ ├── array.c // 顺序表操作实现 用户的航班信息 操作 顺序表操作
│ ├── utils.c // 公用工具函数实现
├── data/
│ ├── users.txt // 用户数据文件
│ └── flights.txt // 航班数据文件
├── img/
│ └── 项目功能图.png // 项目功能图
└── README.md // 项目说明文档
项目介绍书
项目说明书
简历 项目介绍
项目名称 航班管理系统
开发环境
C语言 、 Ubuntu 、 vscode 、 makefile 、 gcc/gdb
项目功能说明
.... 言简意赅
AI 的询问方式 全面的写上项目的功能 让AI 给你 简洁 明了 全面
生产完成后 开另一个对话框
项目流程图
git地址